Как решить дифференциальные уравнения на matlab?

@clement.erdman лучше всего воспользоваться функцией ode45(), она помогает решить дифуры и системы дифференциальных уравнений в подавляющем большинстве случаев.

Привожу пример решения системы линейных дифференциальных уравнений и полученные решения

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

% система линейных дифференциальный уравнений:
% y1'=0.4*t;
% y2'=3-t;


tspan = [0 5]; % диапазон получения решения
y0 = [0 1]; % начальные значения
[t,y] = ode45(@(t,y) [0.4*t; 3-t], tspan, y0);


plot(t,y,'-o'); grid on;


title('Решение системы дифференциальных уравнений');
xlabel('t');
ylabel('y');
legend('y1', 'y2', 'location', 'best');
saveas(gca, 'ODE1.jpg'); 

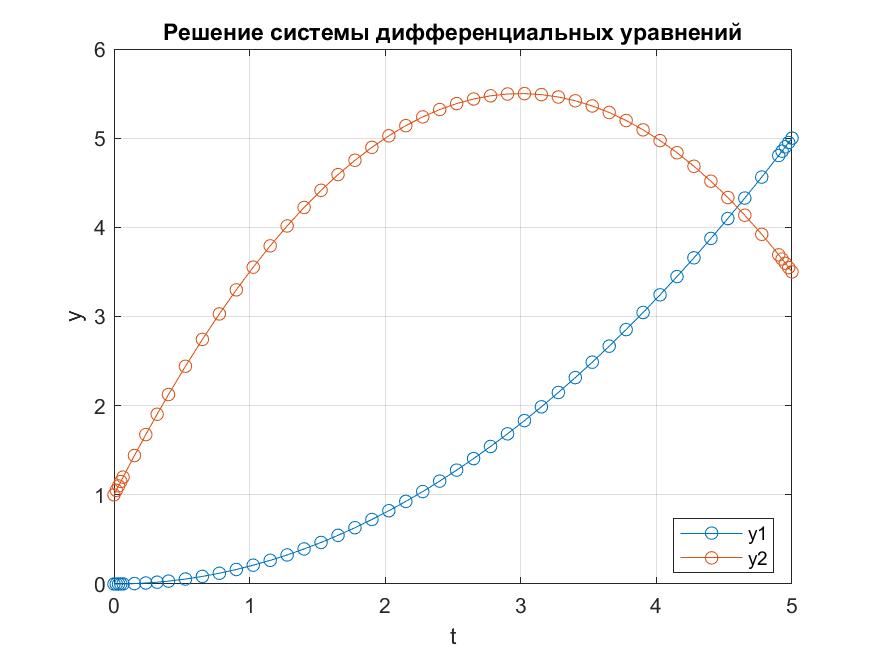
@clement.erdman 

Для решения дифференциальных уравнений на MATLAB можно использовать функции ode45, ode23, ode113, ode15s и другие. Эти функции основаны на методах Рунге-Кутты и Адамса, и могут решать обыкновенные дифференциальные уравнения первого, второго, третьего и более высоких порядков, а также системы дифференциальных уравнений.

Пример решения уравнения y' + 3y = 2sin(x) с начальным условием y(0) = 1:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

% Задание уравнения и начальных условий
dydx = @(x,y) -3*y + 2*sin(x);
x0 = 0;
y0 = 1;

% Решение уравнения
[x,y] = ode45(dydx, [x0, 10], y0);

% Отображение решения
plot(x,y);
xlabel('x');
ylabel('y');

Функция ode45 принимает в качестве первых двух аргументов функцию, описывающую дифференциальное уравнение, интервал интегрирования и начальное значение y. В данном примере решение ищется на интервале от 0 до 10. Результаты решения сохраняются в массивах x и y, которые могут быть использованы для построения графика.