Как найти корень уравнения в matlab?

@guillermo Если уравнение представляет собой полином (или многочлен), то конечно удобнее всего найти корни через функцию roots(), задав значения коэффициентов

1
2

% 2*x^2-16*x+14=0;
roots([2 -16 14]);

получим в ответе 7 и 1.

Если уравнение задано в общем виде, то проще всего воспользоваться символьными вычислениями и решателем vpasolve()

1
2
3
4
5

syms x
f1(x) = 2*x^2-1/x+exp(x);
vpasolve(f1)
fplot(f1); grid on;
saveas(gca, 'out1.png'); 

В ответе получим высокой точности корень:   ans = 0.48082057254304785525398632869782

График этой функции:

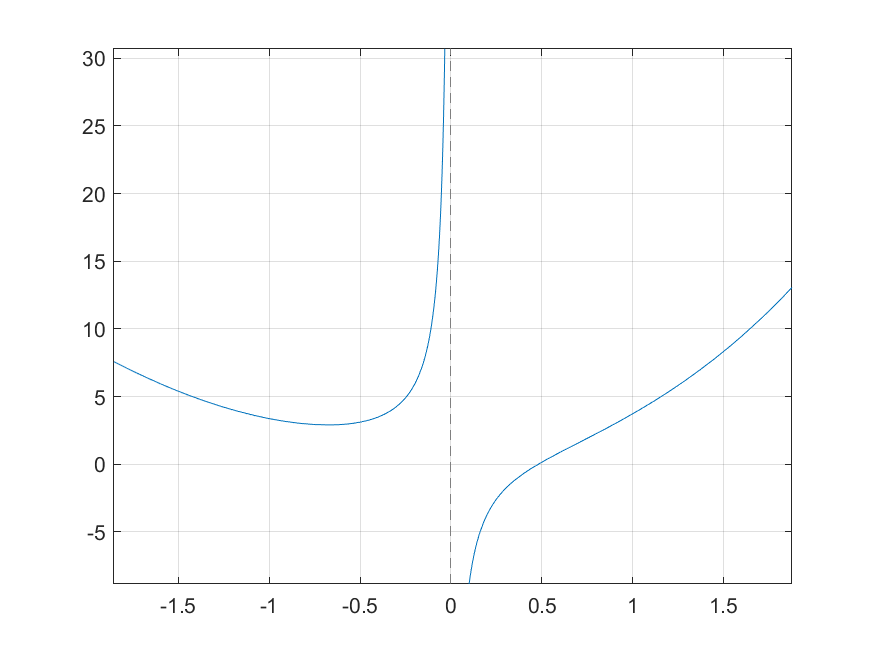
Также можно найти нули функции при помощи функции fzero(), но у этого решения есть некоторые ограничения -- функция не должна уходить в бесконечность и даёт максимум 1 корень.

@guillermo 

Есть несколько способов найти корень уравнения в Matlab, два наиболее часто используемых способа:

1. Использование функции fzero: Функция fzero решает уравнение f(x) = 0 численным методом, начиная с заданной точки. Синтаксис функции fzero: x = fzero(fun,x0), где

• fun - имя функции, которая возвращает значение функции, которую нужно решить
• x0 - начальное приближение для корня

Например, для решения уравнения x^2 + 3x - 7 = 0 можно использовать следующий код:

fun = @(x) x^2 + 3*x - 7; x0 = 1; % начальное приближение x = fzero(fun,x0)

1. Использование символьных вычислений: Matlab имеет инструменты для символьных вычислений, которые позволяют находить корни уравнений аналитически. Для решения уравнения можно использовать функцию solve. Синтаксис функции solve:

x = solve(equation)

где equation - уравнение, которое нужно решить.

Пример использования функции solve для решения уравнения x^2 + 3x - 7 = 0:

syms x % объявляем символьную переменную eqn = x^2 + 3*x - 7 == 0; % задаем уравнение sol = solve(eqn,x) % находим корни уравнения